

El concepto de ocupacion y su modelado
Modelo estatico de ocupacion
Diego J. Lizcano, Ph.D.
Unillanos, Villavicencio
Modelos y simulaciones en ecología
Un modelo en ecología es la descripción matemática de un sistema ecológico.
Cuando la descripción se hace con un propósito practico se llama simulación.
Mas sobre modelos en ecología
Las simulaciones son versiones simplificadas de un sistema real, en el cual podemos probar como varían ciertos parámetros, que afectan los estimados de otros parámetros.
All models are wrong but some are useful.
George Box, 1978. British statistician.
Statististics prof. Univ Princeton
Student of Egon Pearson
Box-Cox transformation
Mas sobre George Box

Por que son útiles las simulaciones:
- Conozco los parámetros verdaderos.
- Son una buena forma de aprender.
- Podemos calibrar un modelo.
- Al ser capaces de simular datos bajo cierto modelo, se garantiza que uno entiende el modelo, sus restricciones y limitaciones.
- Permiten verificar la calidad de los estimados, así como la precisión y el efecto del tamaño muestral.
- Podemos visualizar que tan identificables son los parámetros en modelos más complejos.
Vamos a realizar una simulación de la ocupación (\(\psi\)) y la detectabilidad (p).
Imitar la forma como se originan las medidas de interes. La ocupación (\(\psi\)) y la detectabilidad (p).
Aproximación mecanistica (mecanismo).
Hay dos procesos
Proc. ecológico z.
El cual gobierna la presencia de la especie.
- La especie está (z=1), o no está (z=0) en el sitio. Simulado a partir de una distribución Bernoulli.
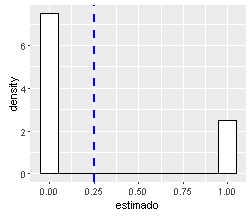
Proc. de observación y.
El cual gobierna la observación de la especie.
- La especie se observa (p=1), si es que la especie esta presente. Prob. condicional. Simulado con una distribución Bernoulli.
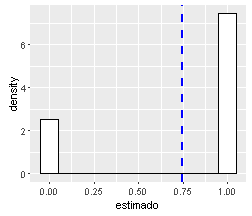
Es importante entender que ambos procesos que se enlazan forma jerarquica.

El proceso ecológico (\(\psi\)) sigue una distribución Bernoulli.
El modelo de observación (\(p\)) sigue una distribución Bernoulli.
La probabilidad de ocurrencia tambien es tambien una proporcion (ocupación):
\(\psi\) = Pr(\(z_{i}\)=1)
- La probabilidad de observar la especie dado que la especie esta presente es:
\(p\) = Pr(\(y_{i}\)=1 \(\mid\) \(z_{i}\)=1)
Ahora jugemos un poco con la distribución Bernoulli
Es una variación de la distribución binomial
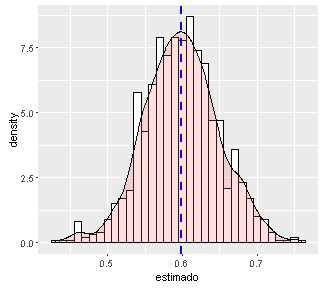
Variemos ni y pi y observemos como la media estimada (azul) se acerca a pi
ni<-10 # numero de datos
pi<- 0.5 # probabilidad (~proporcion de unos)
# Generemos datos con esa informacion
daber<-data.frame(estimado=rbinom(ni, 1, pi))
# Grafiquemos
library(ggplot2)
ggplot(daber, aes(x=estimado)) +
geom_histogram(aes(y=..density..), # Histograma y densidad
binwidth=.1, # Ancho del bin
colour="black", fill="white") +
geom_vline(aes(xintercept=mean(estimado, na.rm=T)),
color="blue", linetype="dashed", size=1) # media en azul
Cambiemos la aproximación. Estudiemos la relación a partir de los datos y las covariables
Relación parametros y covariables
Ocupación y covariables
La ocupación (\(\psi\)) es un conjunto de 1s y 0s.
Las covariables pueden ser continuas o discretas.
| sitio | psi | cov1 | cov2 | cov3 |
|---|---|---|---|---|
| 1 | 1 | 10 | 1.5 | bosque |
| 2 | 0 | 15 | 1.1 | cafe |
| 3 | 1 | 20 | 5.5 | bosque |
| 4 | 0 | 30 | 2.1 | cacao |
| 5 | 0 | 40 | 2.2 | bosque |
Regresión logistica
Observación y covariables
La Observaciones son un conjunto de 1s y 0s.
Las covariables pueden ser continuas o discretas.
| obs | cov1 | cov2 | cov3 |
|---|---|---|---|
| 1 | 10 | 1.5 | nublado |
| 0 | 15 | 1.1 | soleado |
| 1 | 20 | 5.5 | nublado |
| 0 | 30 | 2.1 | nublado |
| 0 | 40 | 2.2 | soleado |
Regresión logistica
Regresión logistica
data(mtcars)
obs<-mtcars$vs
cov1<-mtcars$mpg
table3<-cbind.data.frame (obs,cov1)
library(ggplot2)
ggplot(table3, aes(x=cov1, y=obs)) + geom_point() +
geom_smooth(method = "glm", method.args = list(family = "binomial"))
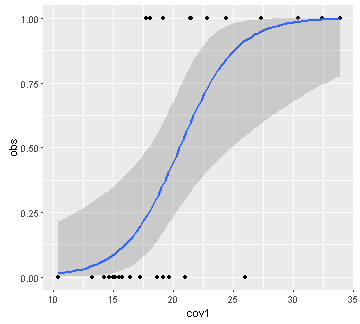
Regresión logistica permite encontrar la relación entre una variable binaria y covariables.
La regresion logistica tiene la forma:
\(y = { 1 \over 1 + e^{ -(\alpha + \beta_1 X_1 + \beta_2 X_2 + \cdots + \beta_p X_p + \epsilon) } }\)
Aplicando el "truco algebraico" de la funcion logit, adopta la forma:
$ logit(y) = \alpha + \beta_1 X_1 + \beta_2 X_2 + \cdots + \beta_p X_p + \epsilon$
Poniendo todo junto...
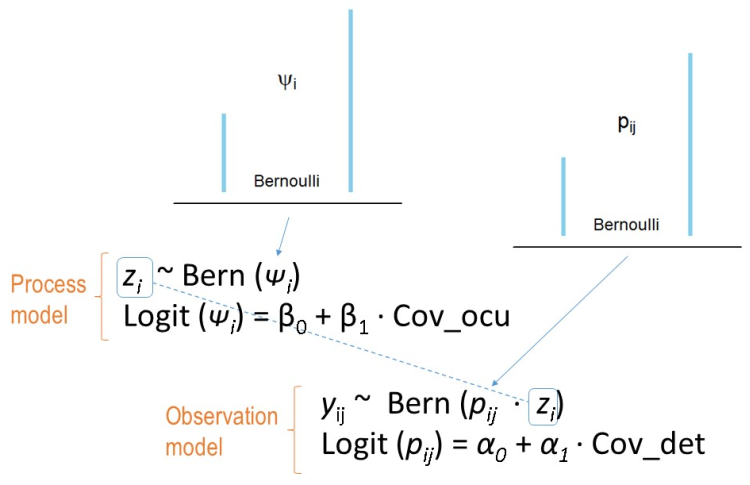
- Pasar a modelo occu en unmarked
Cronograma
| Día | Tema |
|---|---|
| Jueves | 1. Introducción a R |
| 2. R como herramienta de modelado | |
| Viernes | 3. El concepto de ocupación y su modelado |
| 4. Modelo occu. estático - unmarked101 | |
| Sab Mañ | 5. Modelo occu. estático - Sim Machalilla |
| 6. Modelo occu. estático - Unm Machalilla | |
| Sab Tar | 7. Modelo occu. estático - Bayes Machalilla |
| Dom Mañ | 8. Modelo occu. dinámico - Unmarked |
| 9. Preguntas y Datos del mundo real - Pecari | |
| Dom Tar | 10. Otros modelos jerárquicos - Evaluación |
