10.1 Binomial

Recordemos la ecuación de la distribución Binomial:

\[\begin{equation} P\left( x \right) = \frac{{n!}}{{k!\left( {n - k} \right)!}}p^k q^{n - k} = \left( {\begin{array}{*{20}c} n \\ k \\ \end{array}} \right)p^k q^{n - k} \tag{9.1} \end{equation}\]

Donde: \(n\) es el número de ensayos. \(k\) es el número de éxitos. \(p\) es la probabilidad de exíto en un ensayo. \(q=1-p\) es la probabilidad de fracasar en un ensayo.

Por favor no se asuste por la aparente complejidad de la ecuación. Para simplificar la interpretación usaremos en lugar de la ecuación, el álgebra del modelo. Si desea aprender un poco mas de la distribución binomial le recomiendo el video que ha preparado Khan Academy. con un interesante acento mexicano.

\[\begin{equation} P\left( x \right) \sim \mathbf{Bin}(n,p) \tag{9.1} \end{equation}\]

\(P(x)\) es la probabilidad de un valor especifico de \(x\), el cual se distribuye de forma binomial \(Bin\) con los parámetros: \(n\) que corresponde al número de ensayos y \(p\) a la probabilidad.

A continuación, vamos a generar un set de \(n\) datos con una probabilidad dada \(p\). Estos datos son almacenados en un dataframe y luego visualizados como una distribución de frecuencias. La línea azul representa el promedio de esos datos.

n<-10 # numero de datos
p<- 0.5 # probabilidad (~proporcion de unos)
# Generemos datos con esa informacion 
daber<-data.frame(estimado=rbinom(n, 1, p)) 
# Grafiquemos 
library(ggplot2)
ggplot(daber, aes(x=estimado)) + 
    geom_histogram(aes(y=..density..), # Histograma y densidad 
                   binwidth=.1, # Ancho del bin
                   colour="black", fill="white") + 
        geom_vline(aes(xintercept=mean(estimado, na.rm=T)), 
          color="blue", linetype="dashed", size=1) # media en azul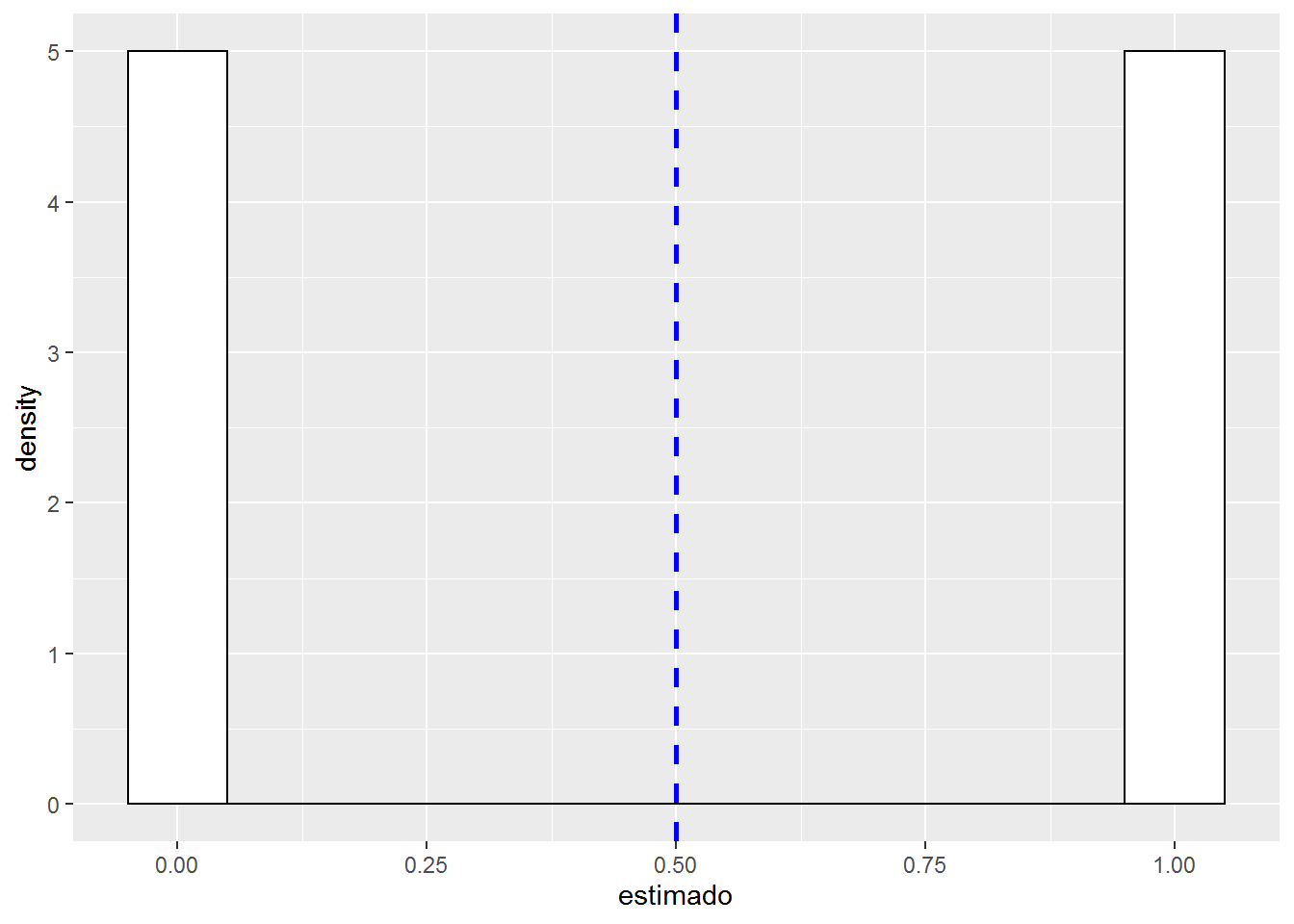

Ejercicio:

Cambie primero el número de datos y luego la probabilidad, haciéndola cercana a cero y luego cercana a uno. Vea como cambia el promedio con el número de datos y la probabilidad.