9.2 Regresión lineal con 2 o más predictores

Ahora haremos las cosas un poco más complejas (sin que sean difíciles) para entender que sucede cuando hay dos o más predictores de la forma:

\[\begin{equation} y = \alpha +\beta_{1}\mathit{x} +\beta_{2}\mathit{x} +\epsilon, \tag{9.1} \end{equation}\]

Usaremos mas (+) para combinar efectos. Dos puntos (:) para interacciones A:B; y asterisco para efectos e interacciones, ej A*B = A+B+A:B

model1a <- lm(Sepal.Length~Petal.Length * Petal.Width, data=iris)
summary(model1a)

## 
## Call:
## lm(formula = Sepal.Length ~ Petal.Length * Petal.Width, data = iris)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -1.00058 -0.25209  0.00766  0.21640  0.89542 
## 
## Coefficients:
##                          Estimate Std. Error t value
## (Intercept)               4.57717    0.11195  40.885
## Petal.Length              0.44168    0.06551   6.742
## Petal.Width              -1.23932    0.21937  -5.649
## Petal.Length:Petal.Width  0.18859    0.03357   5.617
##                          Pr(>|t|)    
## (Intercept)               < 2e-16 ***
## Petal.Length             3.38e-10 ***
## Petal.Width              8.16e-08 ***
## Petal.Length:Petal.Width 9.50e-08 ***
## ---
## Signif. codes:  
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.3667 on 146 degrees of freedom
## Multiple R-squared:  0.8078, Adjusted R-squared:  0.8039 
## F-statistic: 204.5 on 3 and 146 DF,  p-value: < 2.2e-16

library(lattice)

## Warning: package 'lattice' was built under R version
## 4.0.5

newdato<-expand.grid(list(Petal.Length = seq(4, 7, length.out=100), 
                          Petal.Width=seq(1, 2.5, length.out=100)))
newdato$Sepal.Length<-predict(model1a, newdata = newdato) # predice sepalo con petalo de 4 a 7 y 1 a 2.5

levelplot(Sepal.Length~Petal.Length * Petal.Width, data=newdato,
  xlab = "Petal.Length", ylab = "Petal.Width",
  main = "Surface of Sepal.Length")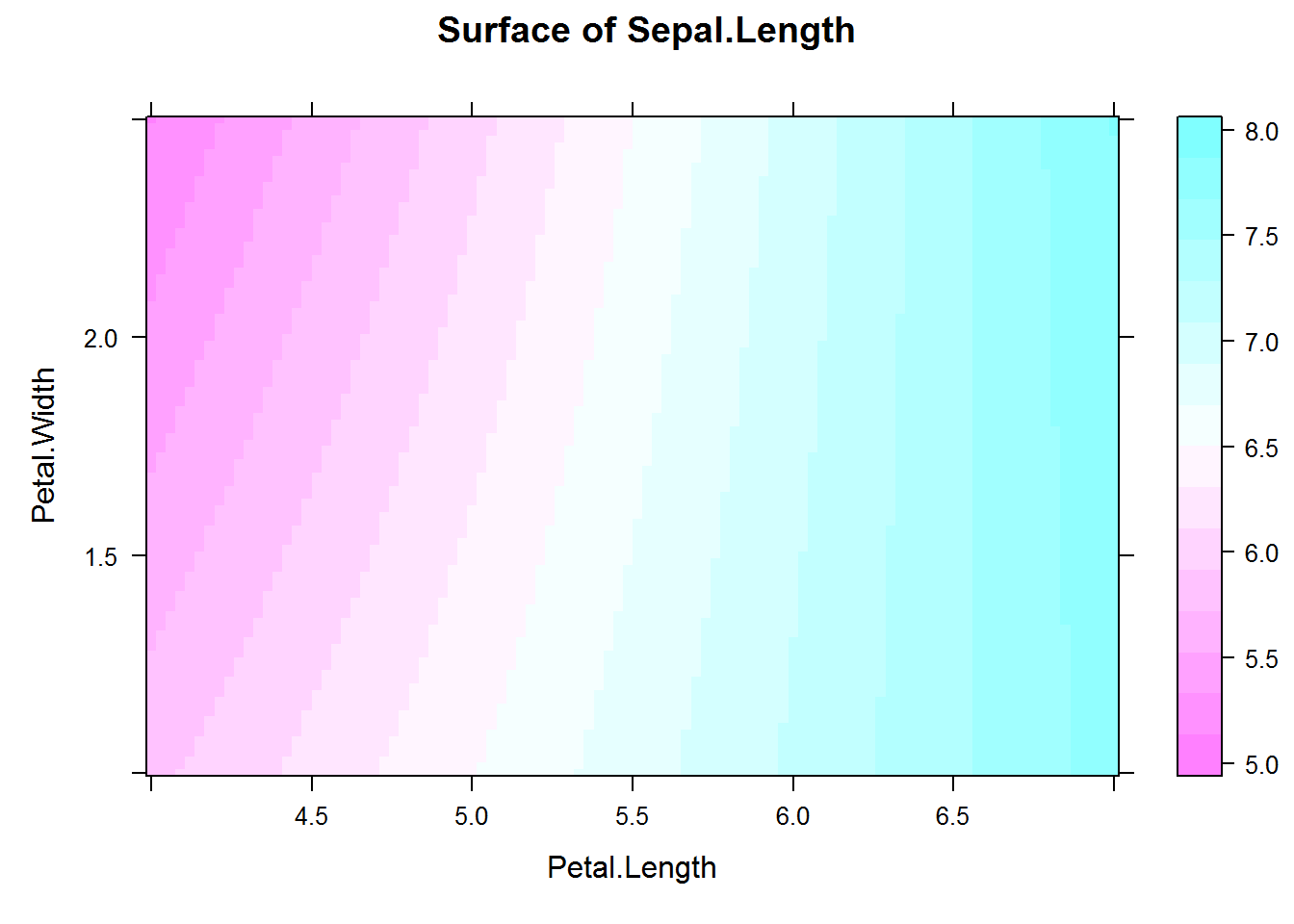

Ejercicio:

Cambie el rango de la predicción de 2 a 8 Cambie en el modelo la interacion de las covariables a +