9.1 Regresión lineal simple

Usaremos el set de datos iris para realizar una regresión lineal entre la longitud del pétalo y la longitud del sépalo.

model1 <- lm(Sepal.Length~Petal.Length, data=iris)
summary(model1)

## 
## Call:
## lm(formula = Sepal.Length ~ Petal.Length, data = iris)
## 
## Residuals:
##      Min       1Q   Median       3Q      Max 
## -1.24675 -0.29657 -0.01515  0.27676  1.00269 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept)   4.30660    0.07839   54.94   <2e-16 ***
## Petal.Length  0.40892    0.01889   21.65   <2e-16 ***
## ---
## Signif. codes:  
## 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.4071 on 148 degrees of freedom
## Multiple R-squared:   0.76,  Adjusted R-squared:  0.7583 
## F-statistic: 468.6 on 1 and 148 DF,  p-value: < 2.2e-16

library(ggplot2)
ggplot(model1, aes(x=Petal.Length, y=Sepal.Length)) + geom_point() + 
  geom_smooth(method = "lm") # try geom_smooth()

## `geom_smooth()` using formula 'y ~ x'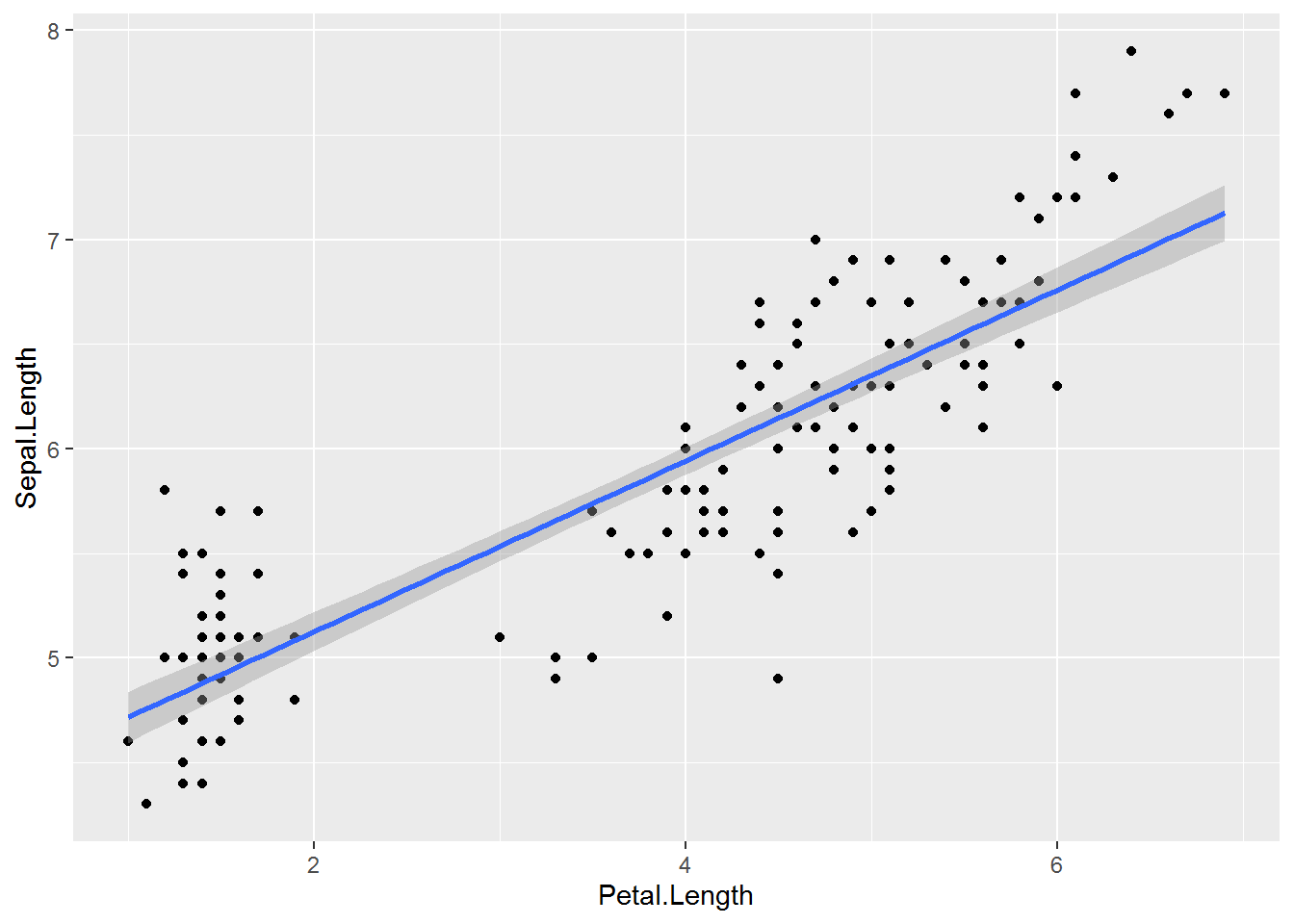

Ejercicio:

Discuta e interprete los coeficientes del modelo.

Ahora utilizaremos el modelo que hemos calculado para predecir cómo se comporta la longitud del sépalo cuando la longitud del pétalo esta entre 2 y 4.

newdato <- data.frame (Petal.Length = seq (2, 4, by = 0.1))
predict(model1, newdata = newdato) # predice sepalo cuando petalo es de 4 a 7

##        1        2        3        4        5        6 
## 5.124448 5.165340 5.206232 5.247125 5.288017 5.328909 
##        7        8        9       10       11       12 
## 5.369801 5.410694 5.451586 5.492478 5.533370 5.574262 
##       13       14       15       16       17       18 
## 5.615155 5.656047 5.696939 5.737831 5.778724 5.819616 
##       19       20       21 
## 5.860508 5.901400 5.942293

Ejercicio:

Use el modelo para predecir el sépalo cuando el pétalo tiene un valor de 7 o mas