8.1 Modelo de la media

Aunque este primer modelo no es un modelo como tal, el siguiente código nos permite entender como el tamaño de la muestra afecta la distribución de la media. Para esto usaremos el set de datos iris de R y la columna largo del pétalo. Lo que haremos será extraer al azar un numero (n) de valores del vector largo del pétalo y calcular la media cien veces. Con estos valores construiremos un histograma.

Haremos una comparación grafica de la forma del histograma con la media (original) del vector largo del pétalo, el cual representaremos con color azul.

str(iris)

## 'data.frame':    150 obs. of  5 variables:
##  $ Sepal.Length: num  5.1 4.9 4.7 4.6 5 5.4 4.6 5 4.4 4.9 ...
##  $ Sepal.Width : num  3.5 3 3.2 3.1 3.6 3.9 3.4 3.4 2.9 3.1 ...
##  $ Petal.Length: num  1.4 1.4 1.3 1.5 1.4 1.7 1.4 1.5 1.4 1.5 ...
##  $ Petal.Width : num  0.2 0.2 0.2 0.2 0.2 0.4 0.3 0.2 0.2 0.1 ...
##  $ Species     : Factor w/ 3 levels "setosa","versicolor",..: 1 1 1 1 1 1 1 1 1 1 ...

iter <- 100 # Numero de iteraciones
n <- 1 # numero de datos que muestreo. Variar hasta 150
means <- rep(NA, iter) # aca almaceno las medias de cada iteracion

for (i in 1:iter){
  d <- sample(iris$Petal.Length, n) # sample toma n (1) datos 
  means[i] <- mean(d) # saca la media y guarda en means 
}

hist(means)
abline(v=mean(iris$Petal.Length), lty=2, lwd=3, col="blue")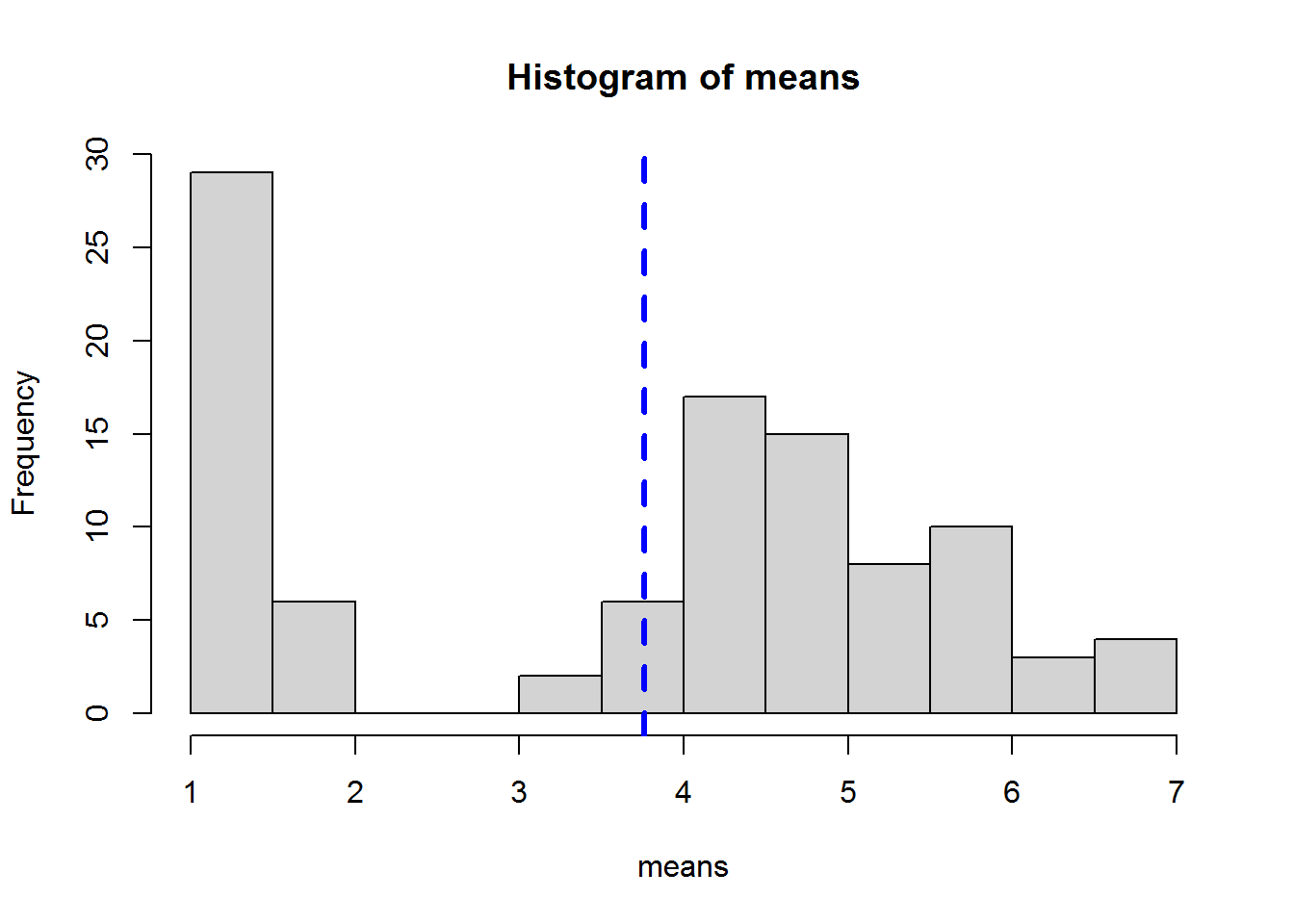

Ahora repitamos el mismo código 10 veces para ver como varia el histograma, ya que estamos seleccioando valores al azar.

Como siguiente paso cambiemos el valor de n a dos (n <- 2), luego a tres, luego cuatro, cinco… etc.

Ejercicio 1

Discuta como varia la forma del histograma en la medida en que el valor de n aumenta.

Ejercicio 2

Convierta el código en una funcion de forma tal que pueda variar el valor de n para producir las graficas en una sola linea.