10.2 Poisson

Recordemos la ecuación de la distribución Poisson:

$$\begin{equation} P\left( x \right) = \frac{{e^{ - \mu } \mu ^x }}{{x!}} \tag{9.1} \end{equation}$$

Donde:

$\mu$ es el número medio de ocurrencia (éxitos) en un intervalo en particular. $e$ es la constante 2.71828 (constante de Euler). $x$ es el numero de ocurrencias (éxitos). $P(x)$ es la probabilidad de un valor especifico de $x$. $!$ es la función factorial.

De igual forma que en la distribución binomial, no nos dejemos intimidar por la complejidad de la ecuación y usemos el algebra del modelo que es mucho más sencilla. Si desea entender un poco mejor el proceso Poisson vean el video que preparó Khan Academy.

$$\begin{equation} P\left( x \right) \sim \mathbf{Pois}(\lambda) \tag{9.1} \end{equation}$$

Donde:

$P(x)$ es la probabilidad de un valor especifico de $x$, el cual se distribuye de acuerdo a la distribución Poisson ($Pois$) y que equivaldría a un valor específico del conteo. $\lambda$ es la media de la distribución.

n <- 100
lambda <- 10
poisson_data <- data.frame('data' = rpois(n, lambda))


library(tidyverse)
poisson_data %>% ggplot() + 
  geom_histogram(aes(x = data, 
                     y = stat(count / sum(count))), 
                     color = 'black',
                 binwidth = 1) +
  geom_vline(xintercept = lambda, 
             size = 1, 
             linetype = 'dashed',
             color = 'red') +
  theme_bw() +
  labs(x = 'Number of successes per period',
       y = 'Proportion',
       title = '1,000 samples of Pois(lambda = 10)')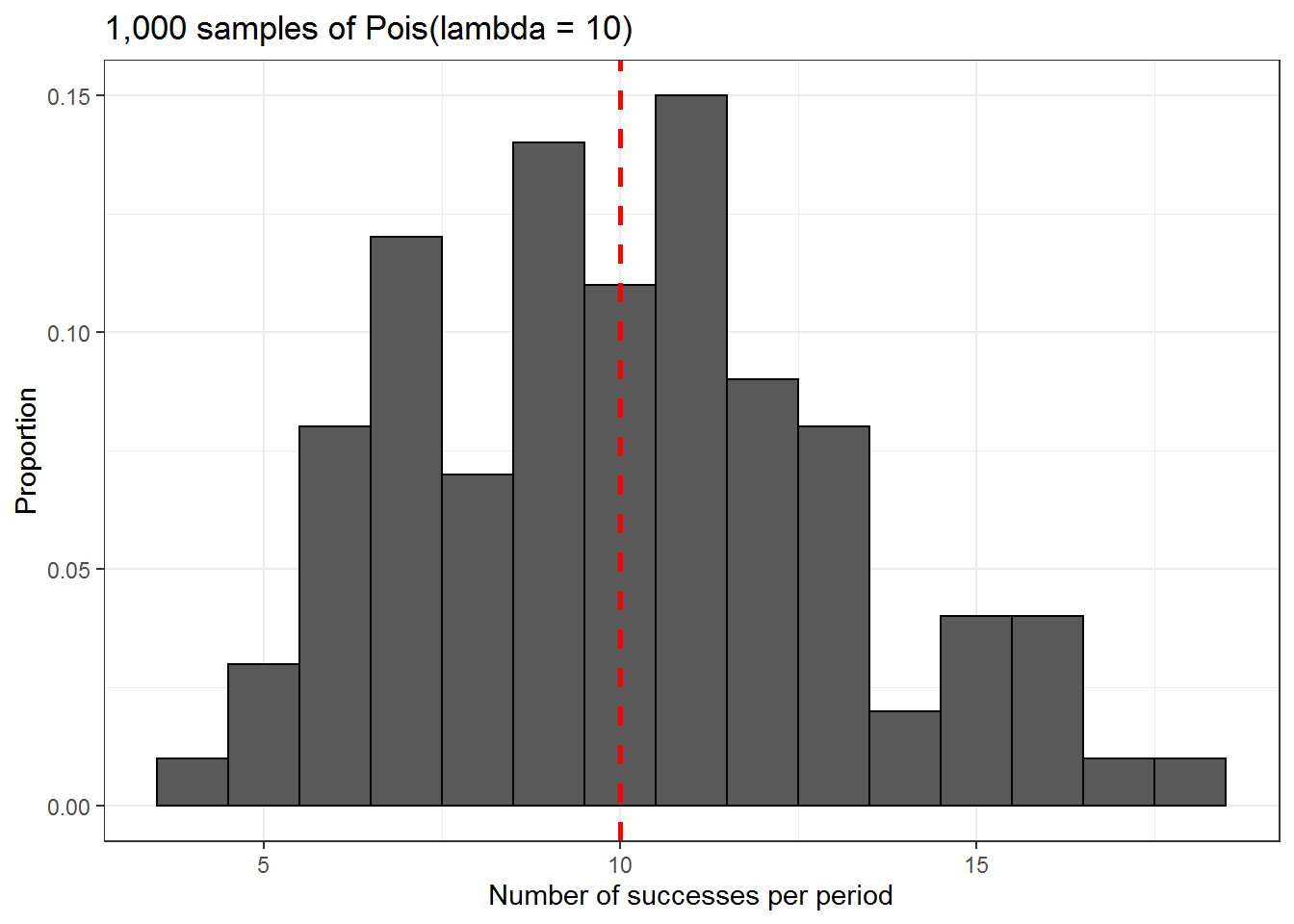

Ejercicio:

Use el modelo para variar n y lambda… vea que sucede.